こんにちは、「学ぶことは真似ることから」まねこです。
今回は小学生で中学受験を検討している方に向けた内容です。
中学受験は多様化が進んでいます。入試に英語を導入することをはじめ、ディスカッション、プログラミングを導入する入試も出現しています。
とはいえ、依然として大半の中学入試の合否は、算数がキーになります。
- 好き嫌いが激しい科目
- 得意不得意がはっきりする
- 入試の配点割合が高い
などの理由が挙げられます。
特に特殊算などの文章問題は、大人でも手こずる問題も多く、多くの子どもが苦戦します。
この算数の文章問題を得意になるたった１つの方法を紹介します。
【中学受験】算数の文章問題を得意にする１つの方法
結論から述べますとズバリこれです。
文章問題を読み、文章の内容を様々な図に表し考える。式に表し答えを導く。
図や式に転換する訓練をすれば、必ず得意になれます。
【小学生の算数】これ解けますか？
突然ですが算数の問題です。
（問題）
スタジアムの開場時刻に、サッカーの試合を観戦するため、すでに長い行列ができています。行列には１分あたり２４人の割合で増えていきます。スタジアムの入り口を３つにすると１時間４０分で行列がなくなり、スタジアムの入り口を４つにすると４５分で行列がなくなります。行列を１５分以内になくすためには入り口を少なくともいくつにすればよいでしょうか。
中学受験を目指している子どもであれば、小学５年生で勉強する人が多い単元です。
受験算数でド定番の問題”ニュートン算”です。
※ニュートン算とは 万有引力の発見でお馴染みのアイザック・ニュートン。 彼の著書の中にあった以下のような問題が起源。 a1 頭の牛は b1 個の牧場の牧草を c1 日で食べつくす。 a2 頭の牛は b2 個の牧場の牧草を c2 日で食べつくす。 a3 頭の牛は b3 個の牧場の牧草を c3 日で食べつくす。 a1～c3の関係を考える
では、(問題)の文章を図に転換して解答していきましょう。
ちなみに、答えは「８つ」となります。小学生の知識だけの解答方法として以下のような解き方があります。
（解答例：）
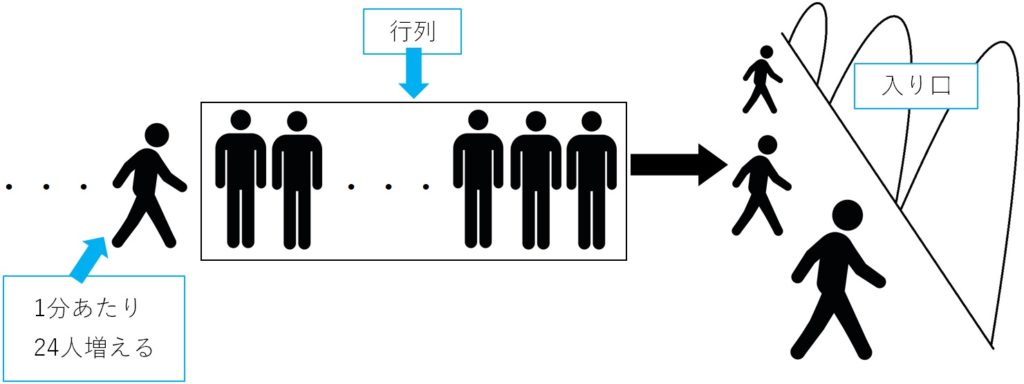
問題を解くときは数秒で書き終えるぐらい”ざっと”でいいです。
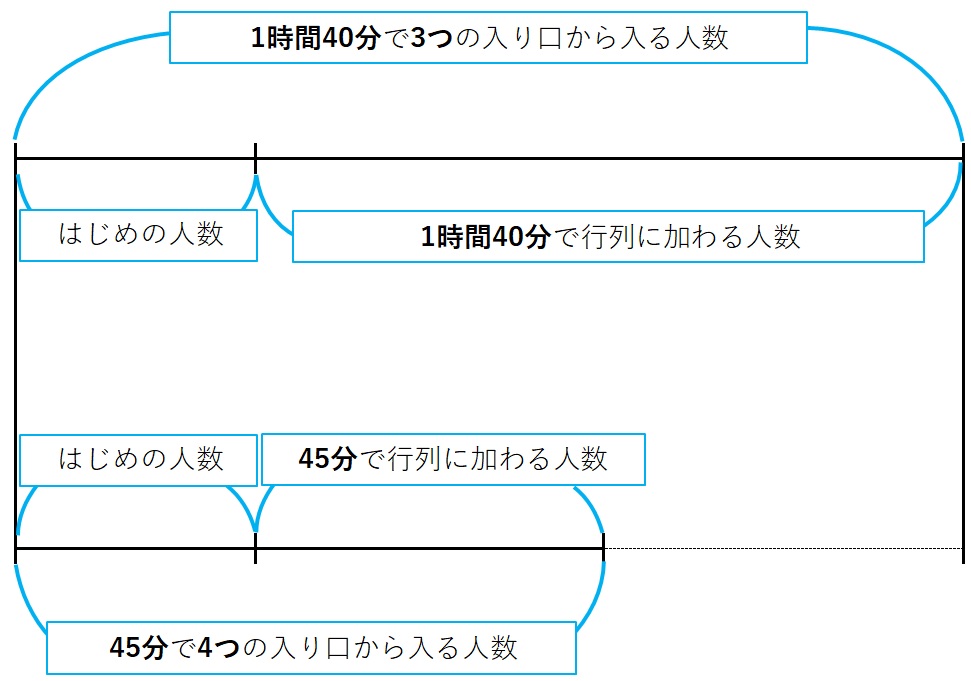
この図を使うと考えが整理できます。頭の中ではイメージできないことが視覚出来きます。順を追って考えていきます。６つの手順です。
1.「１時間４０分で行列に加わる人数」「４５分で行列に加わる人数」を計算する。
- 「 １時間４０分で行列に加わる人数」
１時間４０分=１００分
１分あたり２４人増えるから、２４人×１００分=２４００人
- 「４５分で行列に加わる人数」
同様に、２４人×４５分=１０８０人
２.”１つの入り口から１分間に入る人数を①”として考える（※仕事算の重要な考え方）
「１時間４０分で３つの入り口から入る人数」「４５分で４つの入り口から入る人数 」を計算する。
- 「１時間４０分で３つの入り口から入る人数」
①×３つ×１００分=
- 「４５分で４つの入り口から入る人数」
①×４つ×４５分=
３.１と２の数を図に書き込み、線分図で差を求め書き入れる
- 2400人－1080人=1320人
- ￣ =
この図を書くことによって、にあたる量が1320人と分かる。つまり、
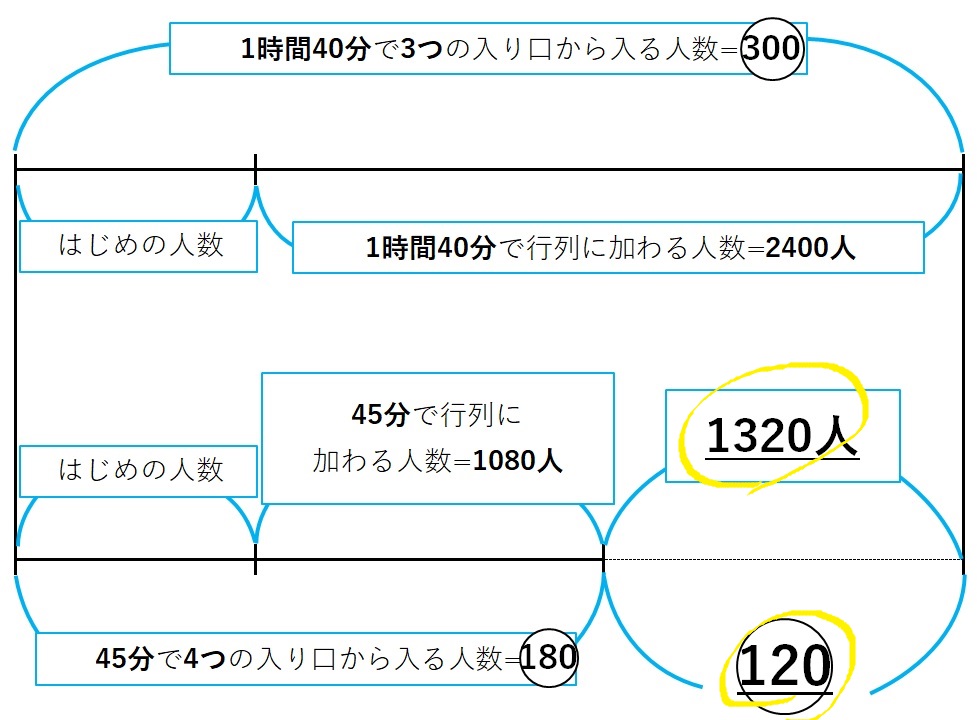
＝1320人
1320人÷=11
①＝11人（①にあたる量が11人）と分かる。
したがって、とにあたる量も計算できる。
- =11人×=3300人
- =11人×=1980人
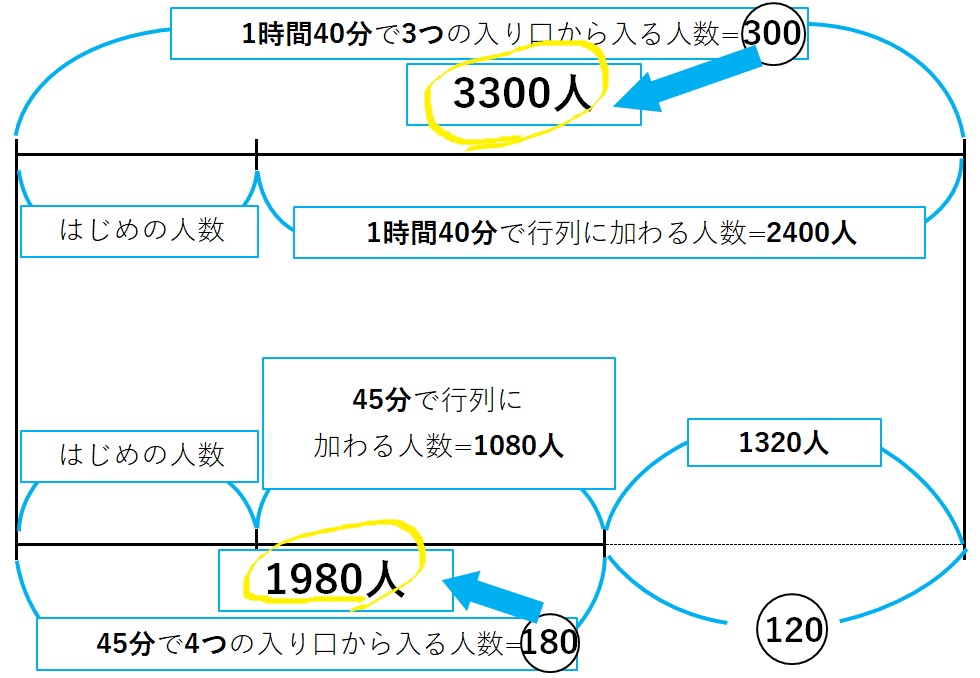
４.線分図の差に注目して「はじめの人数」を求める
- （上の線で考える場合）3300人ー2400人=900人
- （下の線で考える場合）1980人ー1080人=900人
５.１５分以内で行列がなくなるから、１５分間で行列に加わる人数を求め、入り口から入っていく合計人数を考える。
１分あたり２４人の割合で行列に加わるから、
２４人×１５分=３６０人
１５分で３６０人が新たに行列に加わると分かる。
つまり、最初に行列にいた９００人と新たに加わる３６０人の
(900人+360人=)計１２６０人の行列が15分以内になくなればよい。
６.1260人のうち1分あたり何人が入ればよいか求め、入り口の数を求める。
15分以内に行列がなくなればよいから、
1260人÷15分=84人
つまり、1分あたり84人が入り口に入ればよい。
さらに、”１つの入り口から１分間に入る人数は①”、①＝１１人と求めたから、
84人÷11人＝7つあまり7人
よって、15分間で7つ入り口では、7人が入らずあまる。
したがって、1260人が１５分以内に入るには、８つの入り口があればよいと答えがでる。
複雑なことは視覚化せよ
難題ほど、図や式に表して考えるべきです。
先ほどの問題を例に挙げると、まず全体像を掴むために絵を描く。次に数量を線で表し情報を付け加えていく。①あたりの数を求める。線で表したことで、差が明らかになり、考えられることが自然と増えていきます。
先ほどの問題では、頭の中では考えられなかった比較ができ、差について考えることができました。
ニュートン算のような線分図は、初見の人は書くことはできないでしょう。
しかし、経験していくにつれて誰でも書けるようになります。
子どもの場合は、最初は真似をして書いてみる。そして、もう一度同じ問題を解く。さらに、類似問題を解く。
この経験を積むことこそ算数の文章問題が得意になる秘訣です。
逆に言うと算数は書くことをサボると出来るようになりません。
面倒くさがらずに、文章を読み絵や図、式を書く。つまりは視覚化できること。これこそが重要です。
受験算数は図式化が全てといってもいい
図式化によって解く問題は山ほどあります。
- 和差算（線分図）
- 消去算（式化）
- 仕事算（式化）
- 濃度算（天秤図・面積図）
- 旅人算（線分図）
- 流水算（線分図）
- 相当算（線分図）
- 時計算（時計の図）
- 方陣算（碁石の書き並べ）
- 差集め残（線や面積図）
- つるかめ算（面積図）
- やりとり算（線分図）
- 平均算（面積図）
- 損益算（線分図）
小学生の限られた知識・技法で解くには、絵・図は欠かせません。
解法パターンの暗記では将来の中学、高校、大学の勉強に役に立ちません。
単なる暗記ではなく、その後の高度な勉強や研究、仕事の土台となる論理的思考力を中学受験で鍛えるべきです。
算数の考え方を知り、様々な問題に触れ、対応力を鍛えることで思考力はついてくるのではないでしょうか。
では、今回は以上になります。
受験算数の文章問題は得点の差が開きやすい単元です。
合格という目的からしても絶対に逃げては通れません。
また、思考力を養うという目的からしても経験すべきトレーニングです。
「図式」にして文を「見える化」すると思考が進みます。ぜひ参考にしてください。では(^^)/
